See explanation Domain The domain of a function is the largest subset of RR for which the function's formula is defined Given function is a polynomial, so there are no limitations for the values of x This means that the domain is D=RR Range The range is the interval of values which a function takes A quadratic function with a positive coefficient of x^2 takes all values inFigure 3 Domain and range of a function and its inverse When a function has no inverse function, it is possible to create a new function where that new function on a limited domain does have an inverse function For example, the inverse of f ( x) = x \displaystyle f\left (x\right)=\sqrt {x} f (xClick here👆to get an answer to your question ️ Domain and range of f(x) = x 3x 3 are respectively

F X Log 1 3 H A Domain 0 Range B Domain 0 Homeworklib
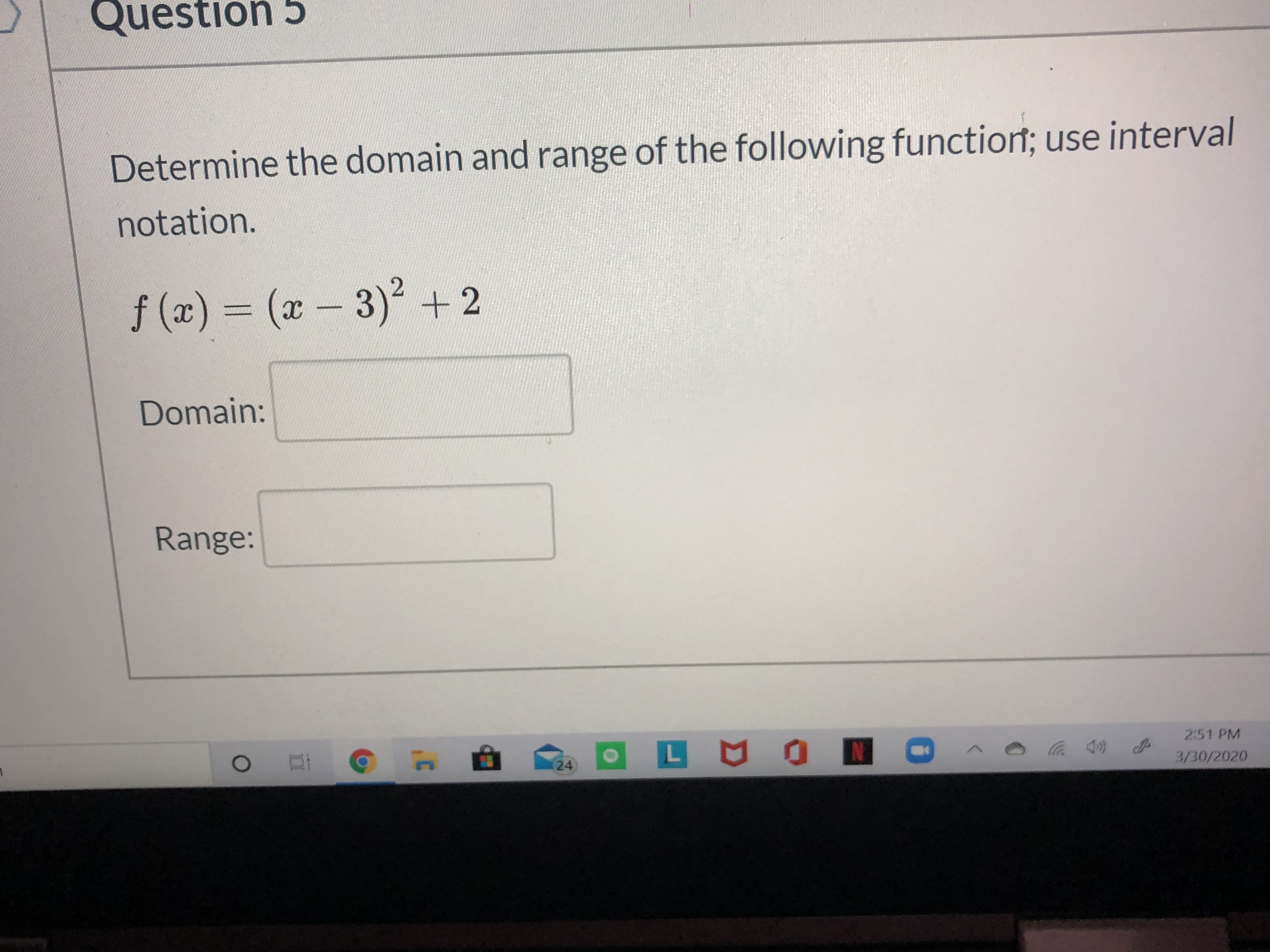
F(x)=x^3-3x+2 domain and range
F(x)=x^3-3x+2 domain and range-How do you find the domain and range of mathf(x)=\frac{3}{2x^2}?/math The domain is the set of values that the independent variable can take In this particular case, the independent variable, mathx,/math can take all the values from theThe domain is all real numbers, and the range is all real numbers f(x) such that f(x) ≤ 4 You can check that the vertex is indeed at (1, 4) Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same y value



2
We have f(x) = (x 2 9)/(x 3) Domain off Clearly f(x) is not defined for x – 3 = 0 ie x = 3 Therefore, Domain (f) = R – {3} Range off Let f(x) = y Then, f(x) = y (x 2 9)/(x 3) = y x 3 = y It follows from the above relation that y takes all real values except 6 when x takes values in the set R – {3} Therefore, Range (f All these are real values Here value of domain (x) can be any real number Hence, Domain = R (All real numbers) We note that that Range f (x) is 0 or negative numbers, Hence, Range = (−∞, 0 Ex 23, 2 Find the domain and range of the following real function (ii) f (x) = √ ( (9 −x^2)) It is given that the function is a real functionFind the Domain and Range f(x)=x^3 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation SetBuilder Notation The range is the set of all valid values
How To Given a function written in equation form, find the domain Identify the input values Identify any restrictions on the input and exclude those values from the domain Write the domain in interval form, if possible Example 332 Finding the Domain of a Function Find the domain of the function f(x) = x2 − 1 The domain of the function f (x) = log3 x (x^2 – 1) is asked in Sets, Relations and Functions by Taanaya ( 236k points) domain and range of a functionX 2 c) ln ( 9 x x 2 ) By signing up, you'll get
Find Domain and Range of real functions (1) `f(x)=(x2)/(3x)` (2)`f(x)=1/sqrt(x5)` (3) `f(x)=x/(1x^2)`Domain and range The domain and range of a function is all the possible values of the independent variable, x, for which y is defined The range of a function is all the possible values of the dependent variable y The example below shows two different ways that a function can be represented as a function table, and as a set of coordinatesSolution For Find the domain and range of f(x) = \dfrac {3x 2}{ x 2} Become a Tutor Blog Cbse Question Bank Pdfs Micro Class Download App Class 11 Math Calculus Relations and Functions II 507 150 Find the domain and range of f (x) = x 2 3 x − 2



Draw The Graph Of The Function F R R Defined By F X X 3 Find Its Domain And Range Sarthaks Econnect Largest Online Education Community




Warm Up State The Domain And Range For If F X X 3 2x 5 Find F 2 Ppt Download
Explanation Because there are no restrictions on the value of x, the Domain of this function is the set of all Real Numbers or {R} Becaue this function is a straight linear transformation, the Range of the function is also the set of all Real Numbers or {R} Answer linkDomain and Range The domain of a function f ( x ) is the set of all values for which the function is defined, and the range of the function is the set of all values that f takes (In grammar school, you probably called the domain the replacement set and the range the solution set They may also have been called the input and output of the function)To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find the domain and range of, `f(x) = 2x33`




Find The Domain And Range Of The Function F X X 2 9 X 3 Brainly In




Find The Domain And Range Of The Function F X Chegg Com
1 Confirm that you have a quadratic function A quadratic function has the form ax 2 bx c f (x) = 2x 2 3x 4 The shape of a quadratic function on a graph is parabola pointing up or down There are different methods to calculating the range of a function depending on the type you are working with given function is f (x)=x2−9x−3 since the denominator can not be zero x−3≠0⇒x≠3 the domain of the function is R− {3} y=f (x)=x2−9x−3y= (x−3) (x3)x−3y=x3 for x∈R− {3}y≠33 f (x) is not defined for x=3y≠6 range of the function is R− {6} hope this helps you dome7w and 86 more users found this answer helpful To find The domain and range of the real function Solution To find domain Equate the denominator to zero Denominator (3x)=0 x=3 This means at x=3 function is not defined And by definition of domain The domain is where the function is not defined Domain is Range Put f(x)=y Range is the set of value that correspond to domain




Domain And Range Of Functions



Domain And Range Examples Domain And Range Of Functions
x >= 3 or in interval notation 3, oo) Given F(x) = sqrt(x 3) A function starts out having a domain of all Reals (oo, oo) A square root limits the function because you can't have negative numbers under the square root (they are called imaginary numbers) This means " "x 3 >= 0 Simplifying " "x >= 3The domain of a function is defined as the input values The range is defined as the output values Answer The domain and the range of the function f (x) = 3x 5 is ( ∞, ∞) Let's find the domain and range of the function Explanation Values of y in f(x) = y determines the range of the functionDomain of a function is the set of all those values of x for which f(x) is a finite real number(Provided we are given a real valued function) Notice that the polynomial 2x1 has a zero at x=1/2 Now if we input this value of x into the function
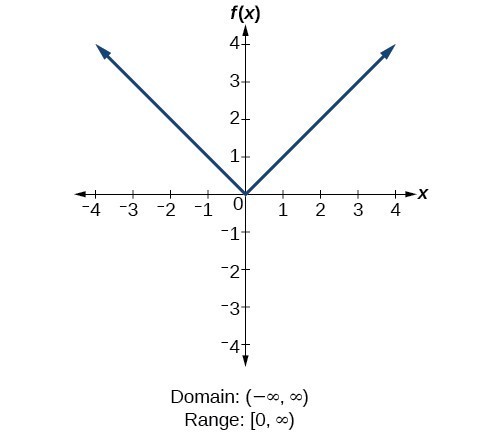



Determine Domain And Range From A Graph College Algebra
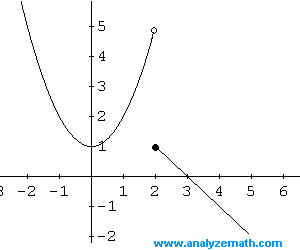



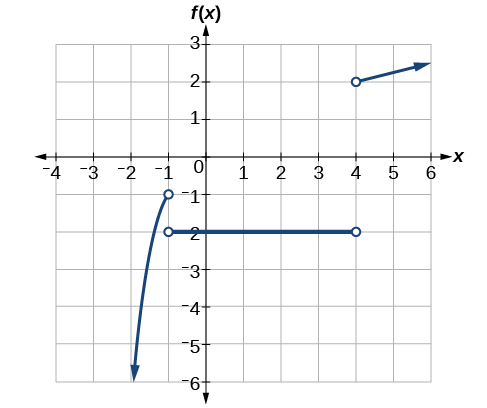
Graph Piecewise Functions
Calculus Find the Domain and Range f (x)=5x3 f (x) = 5x − 3 f ( x) = 5 x 3 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval NotationDOMAIN we know that in squareroot, we cannot have negative values because underoot negative only exist in complex numbers and we are discussing in Real numbers Therefore, in squareroot we can have values greater than or equal to zero X3 musF(x)=2x3 Domain actually stand for input and range is the output Functions can be seen as something in which you give input and it gives you output So domain is the value set or interval for which the function gives out defined result f(x)=2




6 Ways To Find The Domain Of A Function Wikihow



What Is The Domain And Range Of 1 X 3 Quora
I'll be breaking down this question in three parts, 1 When x is positive 2 When x is negative 3 When x is zero In the first case, if x is positive, And since the modulus of a positive number is the number itself, our function becomes, f(x) = x/Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution domain\f(x)=\sqrt{x3} domain\f(x)=\cos(2x5) domain\f(x)=\sin(3x) precalculusfunctiondomaincalculator enFor the cube root function latexf\left(x\right)=\sqrt3{x}/latex, the domain and range include all real numbers Note that there is no problem taking a cube root, or any oddinteger root, of a negative number, and the resulting output is negative (it is an odd function)



2
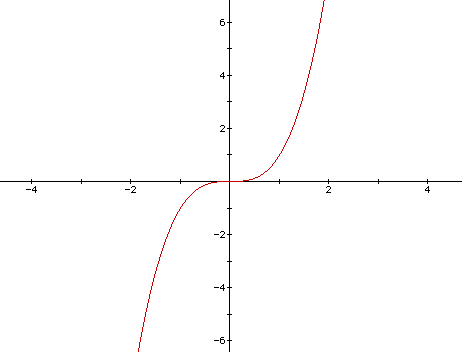



How Do You Find The Domain And Range Of F X X 3 3x 2 Socratic
Algebra Find the Domain and Range f (x)=x^23 f (x) = x2 3 f ( x) = x 2 3 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval NotationTable of Domain and Range of Common Functions A table of domain and range of common and useful functions is presented Also a Step by Step Calculator to Find Domain of a Function and a Step by Step Calculator to Find Range of a Function are included in this websiteFind the Domain and Range f(x)=3 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no
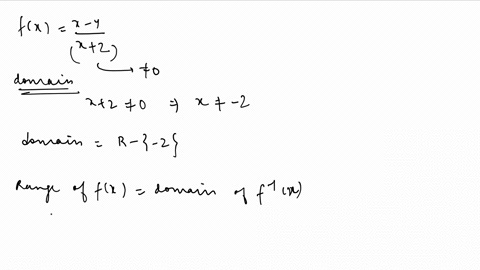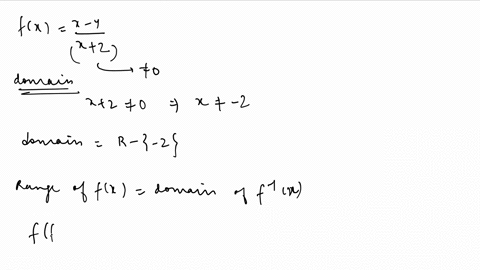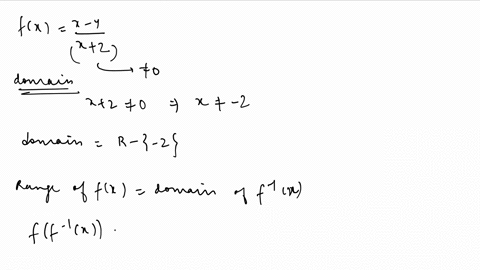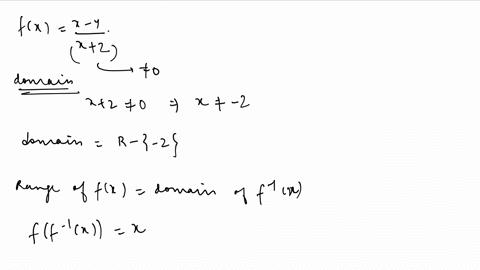



Solved Find The Domain And Range Of The Function




How To Find The Domain And Range Of A Function 14 Steps
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find domain and range of `f(x)=x/(1x^2)`Answer to Find DOMAIN and RANGE of the following a) f(x)= 3 x 3 b) 1 ( 3 ?The domain is obtained by solving(x − 1) (3 − x) ≥ 0 You can obtain the zeroes of the polynomial (x − 1) (3 − x) = 0 If x − 1 = 0 x = 1 If 3 − x = 0 ⇒ x = 3 So, x = 1, 3 So the polynomial is solved in the external intervals x > 1, x > 3 So, x ∈ (1, ∞) Since the function f (x
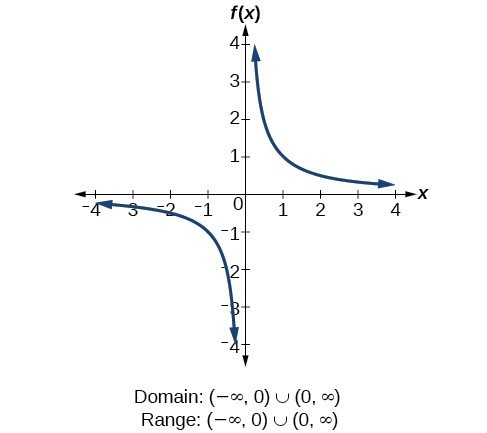



Determine Domain And Range From A Graph College Algebra



Domain Range
Domain is the numbers you can use for x range is the numbers you get from inputing the domain for x we don't see any restrictions (like division by 0 or square roots of a negative) so domain is all real numbers alright so if we try x=infinity, we get that 3 The terms within the radical are x 3 Find domain and range of f (x)= square root of (x 1) (3 x) Enter your answer for the domain using interval notation Set the radicand in greater than or equal to to find where the expression is defined Fx x 2 2 x 1 Solution to Example 3Solution to Example 4 The domain of this function is the set of all real numbers The range is the set of values that f (x) takes as x varies If x is a real number, x 2 is either positive or zero Hence we can write the following x 2 ≥ 0 Subtract 2 to both sides to obtain x 2 2 ≥ 2
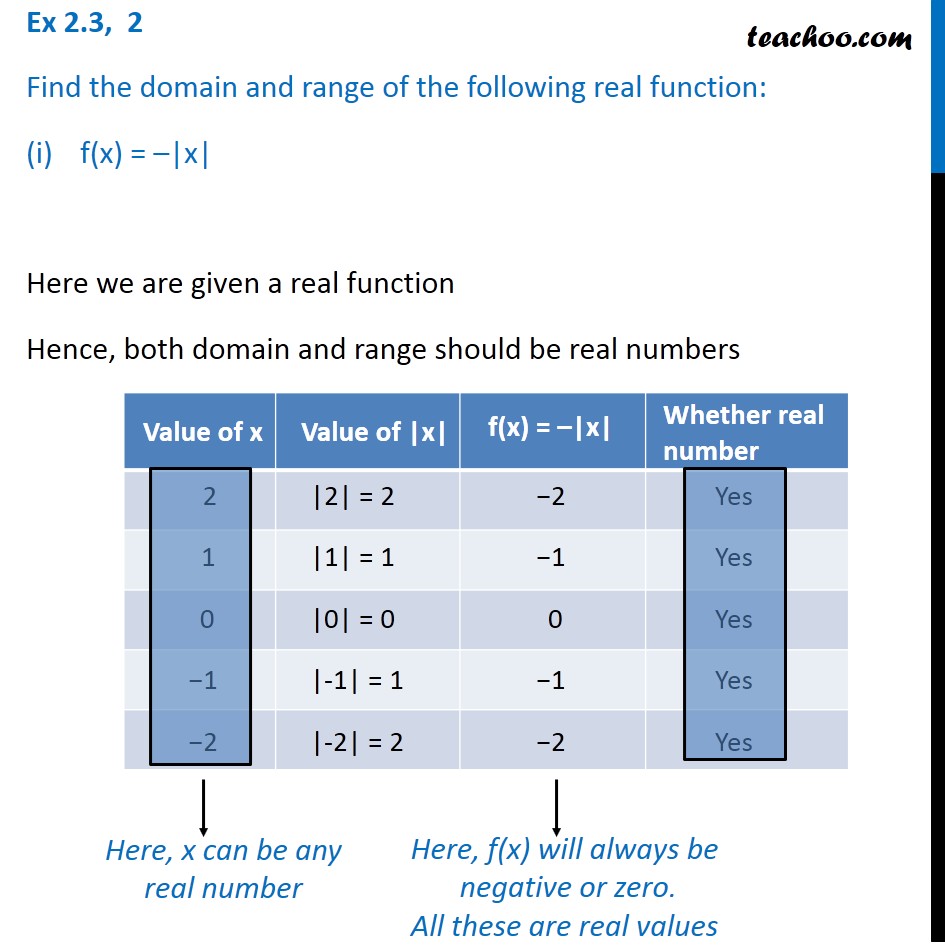



Ex 2 3 2 Find The Domain And Range Of The Function F X X
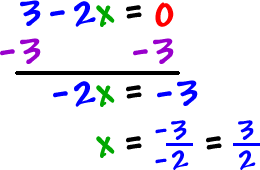



Finding The Domain Of A Function
Substitute 1 into the quadratic to get 1^2 2 (1) 5 = 1 2 5 = 4 Vertex is at (1,4) and it opens upward Since no values of x are negative, domain is all real numbers Then, since the vertex is the low point, take the primary square root of 4 to get 2, so range is y ≥ 2 Given f(x) = 3/(2 x 2) To find the range of function Explanation So, the range of a function consists of all the second elements of all the ordered pairs, ie, f(x), so we have to find the values of f(x) to get the required range Given, f(x) = 3/(2 x 2) Let this be equal to y, soAlgebra Find the Domain and Range f (x)=1/ (x3) f (x) = 1 x − 3 f ( x) = 1 x 3 Set the denominator in 1 x−3 1 x 3 equal to 0 0 to find where the expression is undefined x−3 = 0 x 3 = 0 Add 3 3 to both sides of the equation x = 3 x = 3 The domain is all values of x x that make the expression defined Interval Notation




F X Log 1 3 H A Domain 0 Range B Domain 0 Homeworklib



Domain Range Functions Slope Bingo Card
The domain of a function is defined as the input values for which the function is defined The range is defined as the output values Answer The domain and the range of the function f (x) = 2 (3x) is ( ∞, ∞) Let's find the domain and range of the function Explanation f (x) = y is the range of the function Given, f (x) = 2 (3x) ⇒ fGiven f (x) = 2 − ∣ x − 5 ∣ Domain of f (x) is defined for all real values of x Since, ∣ x − 5 ∣ ≥ 0 − ∣ x − 5 ∣ ≤ 0 2 − ∣ x − 5 ∣ ≤ 2 f (x) ≤ 2 Hence, range of f (x) is (− ∞, 2 Domain All real numbers or (oo, oo) Range All real numbers or (oo, oo) The domain of any graph includes all the xvalues that are solutions The range accounts for all yvalues that are solutions graph{x^3 10, 10, 5, 5} According to this graph of the equation, we see that the xvalues continuously increase while yvalues do the same
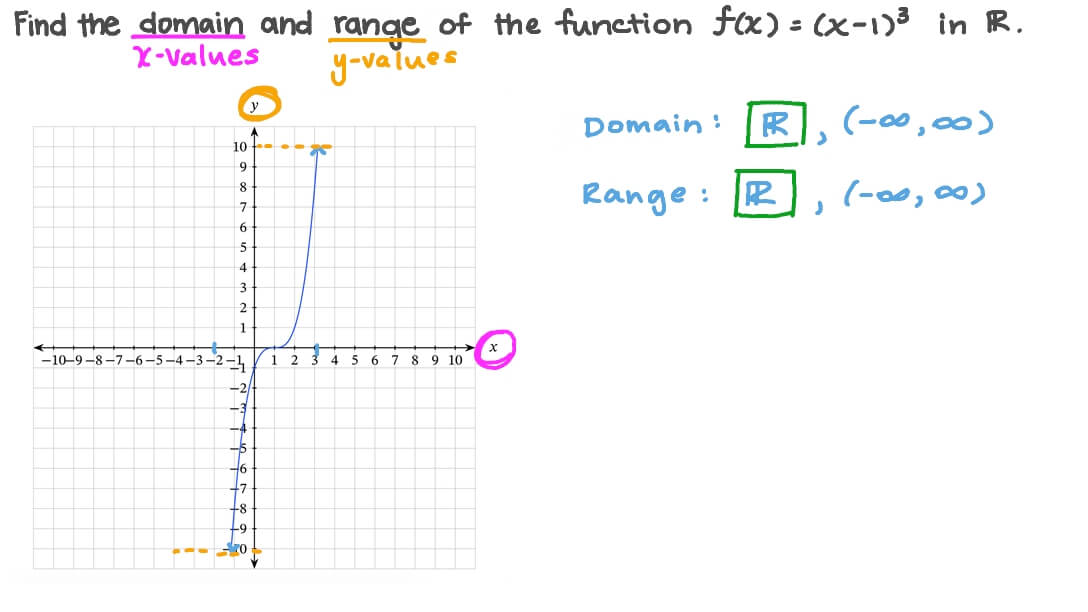



Question Video Finding The Domain And Range Of A Cubic Function Given Its Graph Nagwa
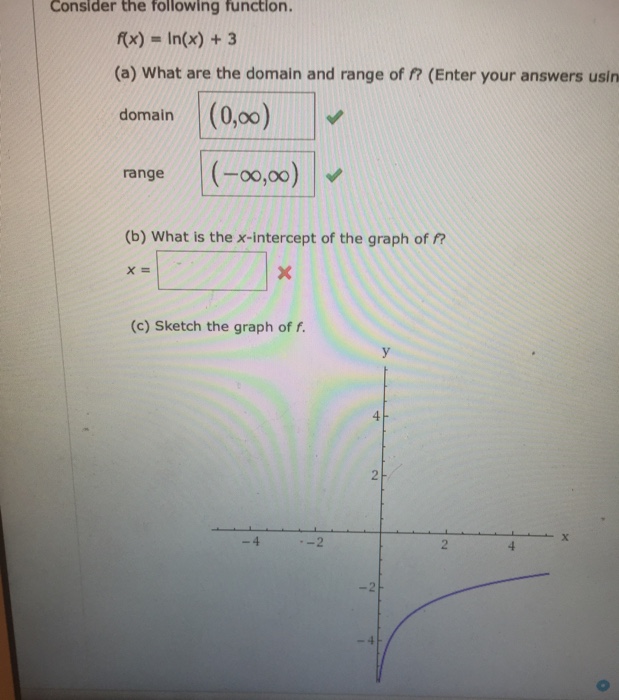



Consider The Following Function F X Ln X 3 Chegg Com
For instance, f (x) = The domain is simply the denominator set equal to 0, {xl x≠3} However, range is found by solving for (isolating x to one side) and setting the denominator equal to zero x = So range is {xl x≠0} This is a systematic method that I assume is the only way to find the range



Domain And Range Of A Relation Worked Out Problems On Domain And Range Range




Finding Domain And Range



Answer In Algebra For Dani Wagas
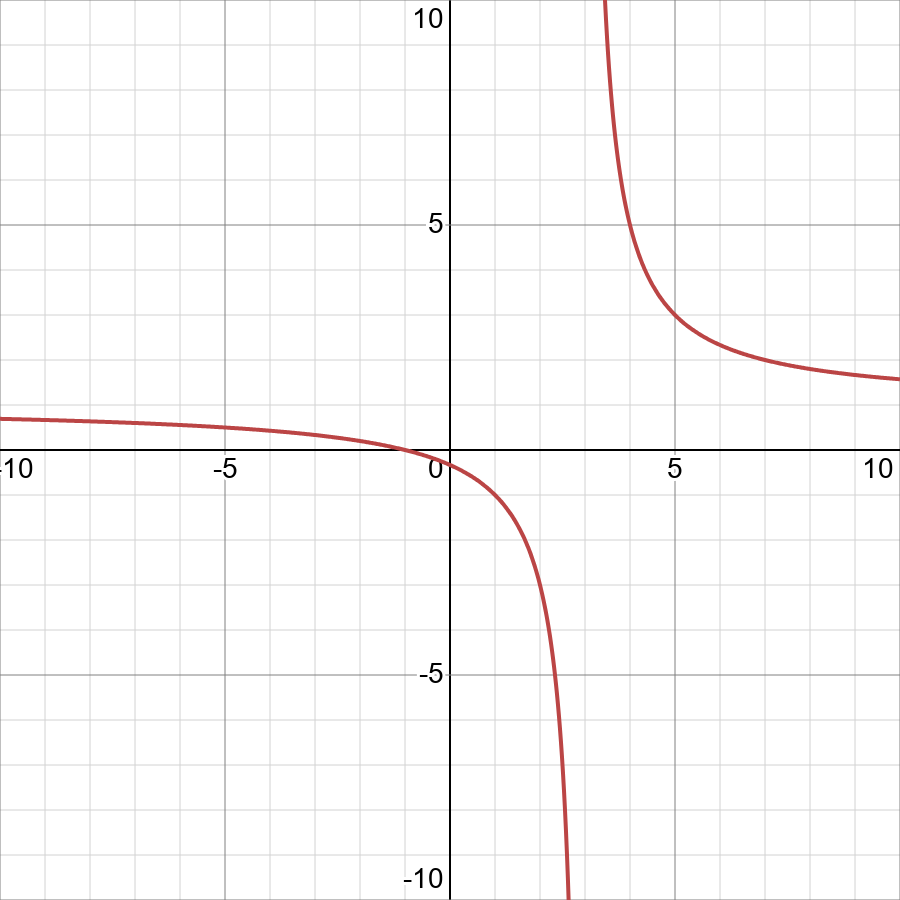



Find The Domain And Range F X X 1 X 3 Displaystyle Fleft Xright Frac X 1 X 3 Snapsolve




How To Find The Domain And Range Of A Function 14 Steps



Search Q Domain Of Square Root Function Tbm Isch




Graph Domain And Range Of Absolute Value Functions




What Is The Domain And Range Of F X Abs X 3 5 2 Socratic




Domain And Range Of A Function Utrgv



What Is The Domain And Range Of Real Function F Defined By F X 1 X 3 Quora



3 3 Domain And Range Mathematics Libretexts



Introduction To Domain And Range Relations And Functions Geeksforgeeks




Domain And Range Of Quadratic Functions Video Khan Academy



Domain And Range Of A Function



Solved What Is The Range Of The Function F X 6x 3 Over The Interval Of 1 X 6 Course Hero




Find The Domain Or Range Of Following Function Tex F X Sqrt X 1 3 X Tex Brainly In




Tex F X Sqrt 3 2x Tex Find Domain And Range Of The Function Brainly In




Domain And Range Free Math Help




Find The Domain And Range Of The Following Functions A F X Frac 1 X 3 B G X Sqrt X 6 C H X X 3 2x 5 Study Com



Domain And Range Examples Domain And Range Of Functions



2




Find The Domain And The Range Of The Real Function F X X 3 X 5 Youtube
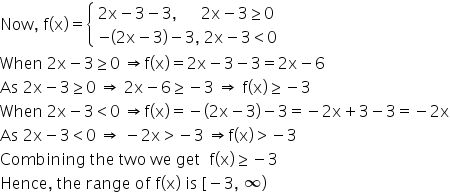



Hello Sir I Need A Full Explanation Of This Sum Find Domain And Range Of F X 2x 3 3 Mathematics Topperlearning Com 4fb8db22
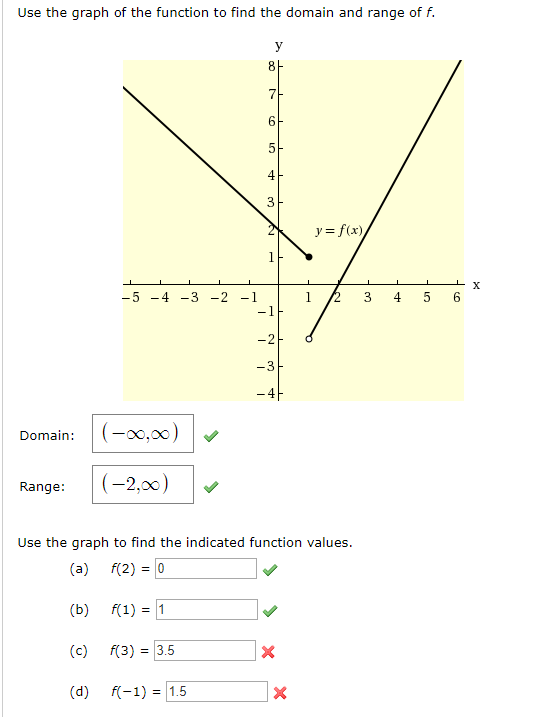



Use The Graph Of The Function To Find The Domain And Chegg Com



2




Find The Domain And The Range Of The Real Function F X X 3 X 3




Domain Range Doubt Maths Doubts Doubtion
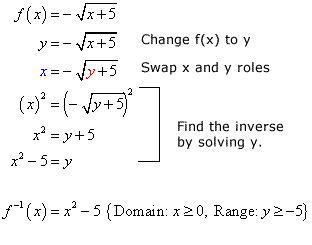



Inverse Of Square Root Function Chilimath
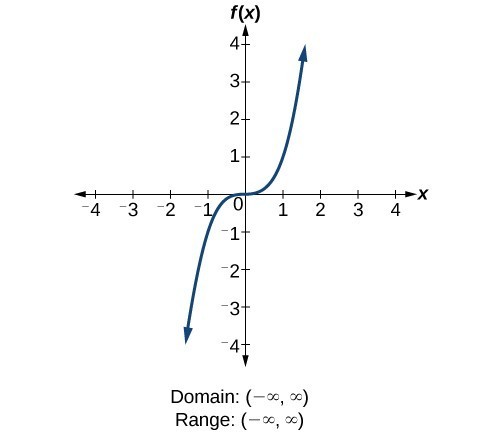



Determine Domain And Range From A Graph College Algebra



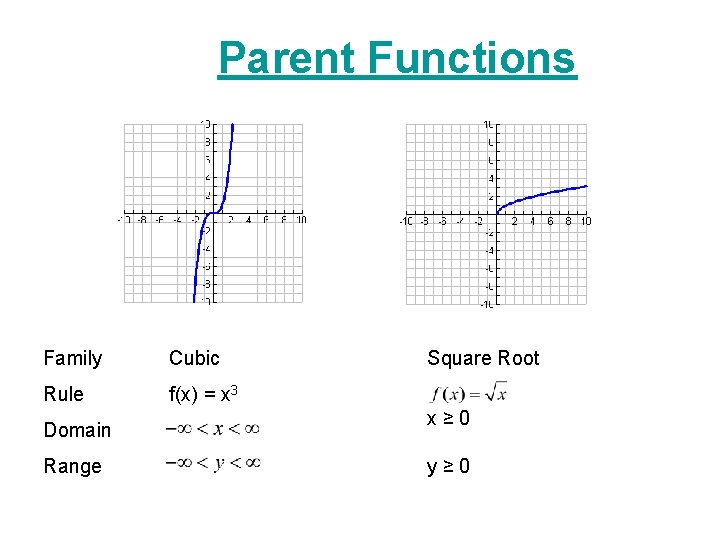
Search Q Parent Functions Tbm Isch



Warm Up 924 For Each Function Evaluate F0




View Question What Are The Domain And Range Of The Function




Find The Domain And Range Of The Real Function F X Sqrt 9 X 2 Youtube
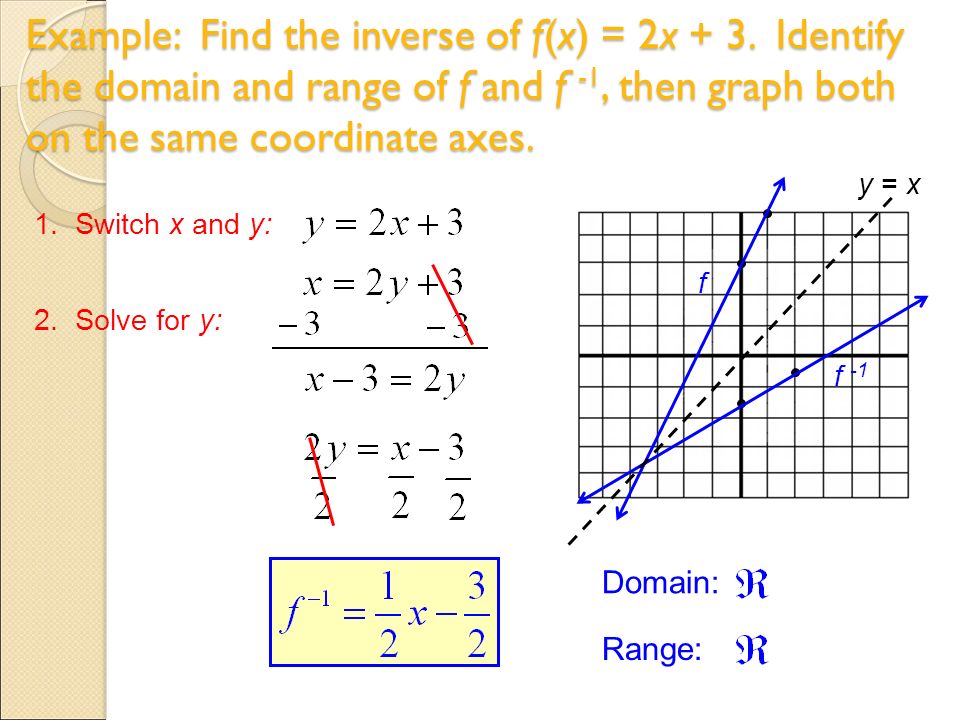



More Quarter Test Review Section 4 1 Composite Functions Ppt Download



How To Find The Domain Range And Roots Of Polynomials And Rational Functions Universalclass




Misc 5 Find Domain And Range Of F X X 1 Class 11




Find The Range Of Each Of The Following Functions F X X 3 F X 1 X 2 F X X 4 Youtube
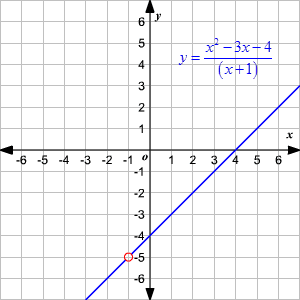



Domain And Range Of Rational Functions



3




How Do You Find The Domain And Range 3 10 Points Find The Inverse Of The Homeworklib



For The Function F X X 2 5 Find The Domain And Range Enotes Com
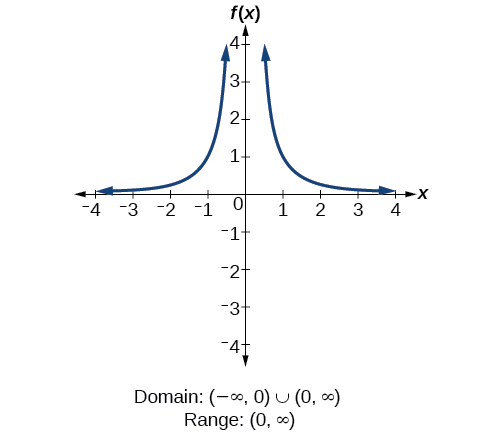



3 2 Domain And Range Mathematics Libretexts



Domain Of Inverse Function Expii




Domain And Range Free Math Help



1




Find The Domain Range And Zeros Of The Function Help Khan Academy Help Center



Answered Determine The Domain And Range Of The Bartleby




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 Youtube




Ppt Review Parent Functions Graph Functions By Shifts Find Domain Range And Intercepts Powerpoint Presentation Id



Solution Find The Domain And Range Of The Inverse Of The Given Function F X Square Root X 3 All Under Square Root A Domain All Real Numbers Range 3 Infinity B Domain 0 Inf




Domain And Range Of F X X 3 X 3 Are Respectively
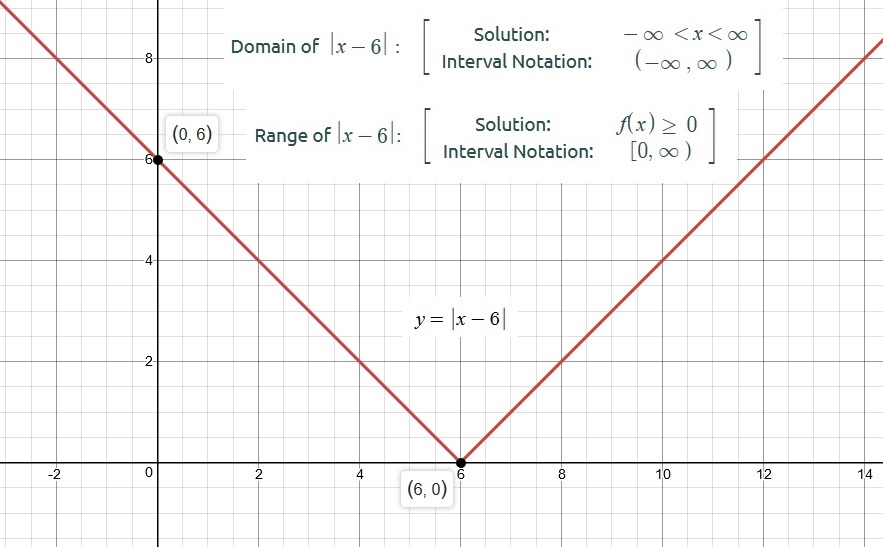



How Do You Find The Domain And Range Of Y X 6 Socratic
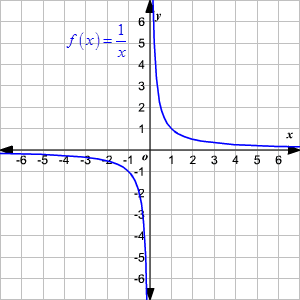



Domain And Range Of Rational Functions




Find The Domain And Range Of The Following Functions I F X X 2 Ii F X X 1 3 X



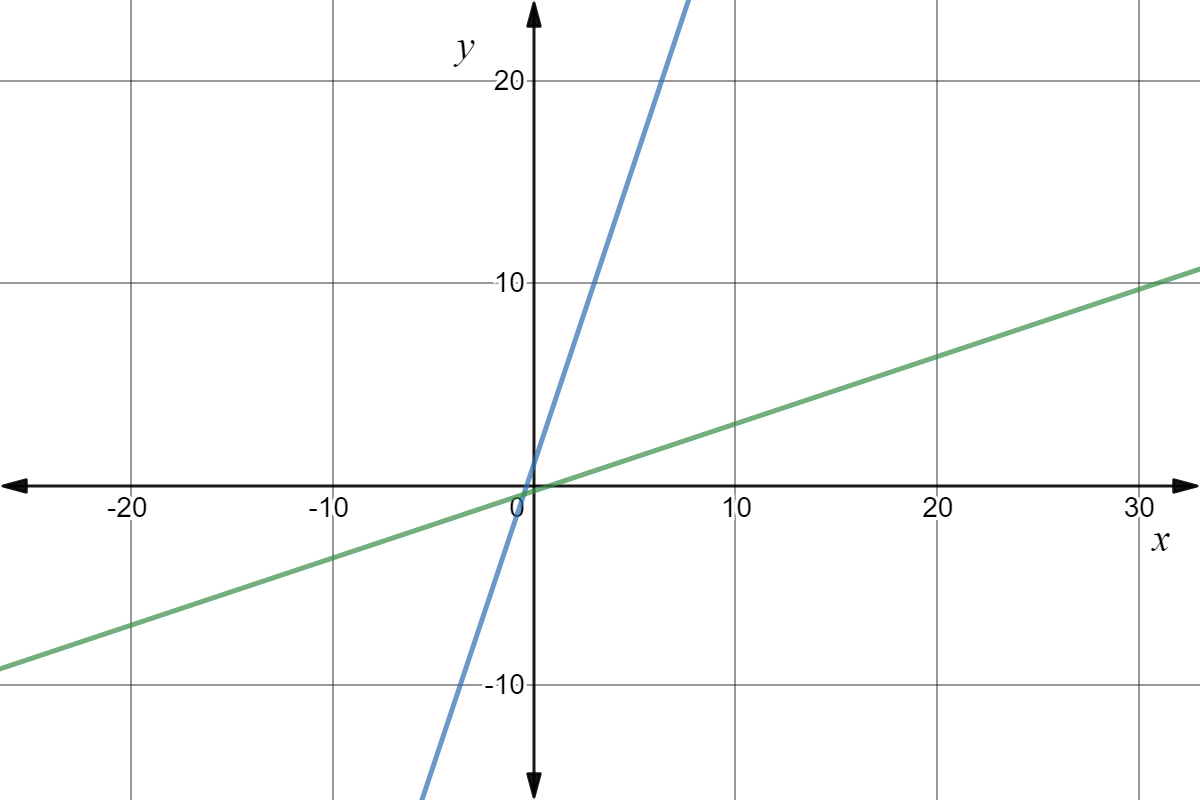
Solution Given That F X 2x 3 Determine The Domain And Range Of This Linear Funtion




Domain And Range Shortcut Rules The Qubits Blog
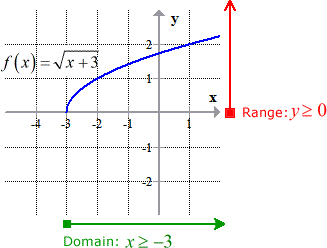



Inverse Of Square Root Function Chilimath




L1 Functions Domain Amp Range




Answered The Function F Has A Domain Of 0 5 Bartleby



Continuity And Differentiability Swl K12 Oh Us




What Is The Range And The Domain Of F X X2 2x 3 Brainly Com




Find The Domain And Range Function F X X 2 3x 2 X 2 4x 3
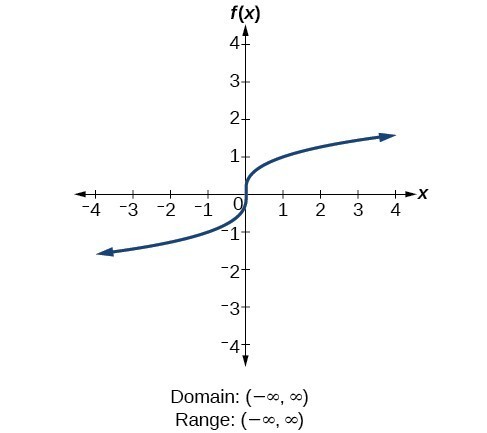



Determine Domain And Range From A Graph College Algebra
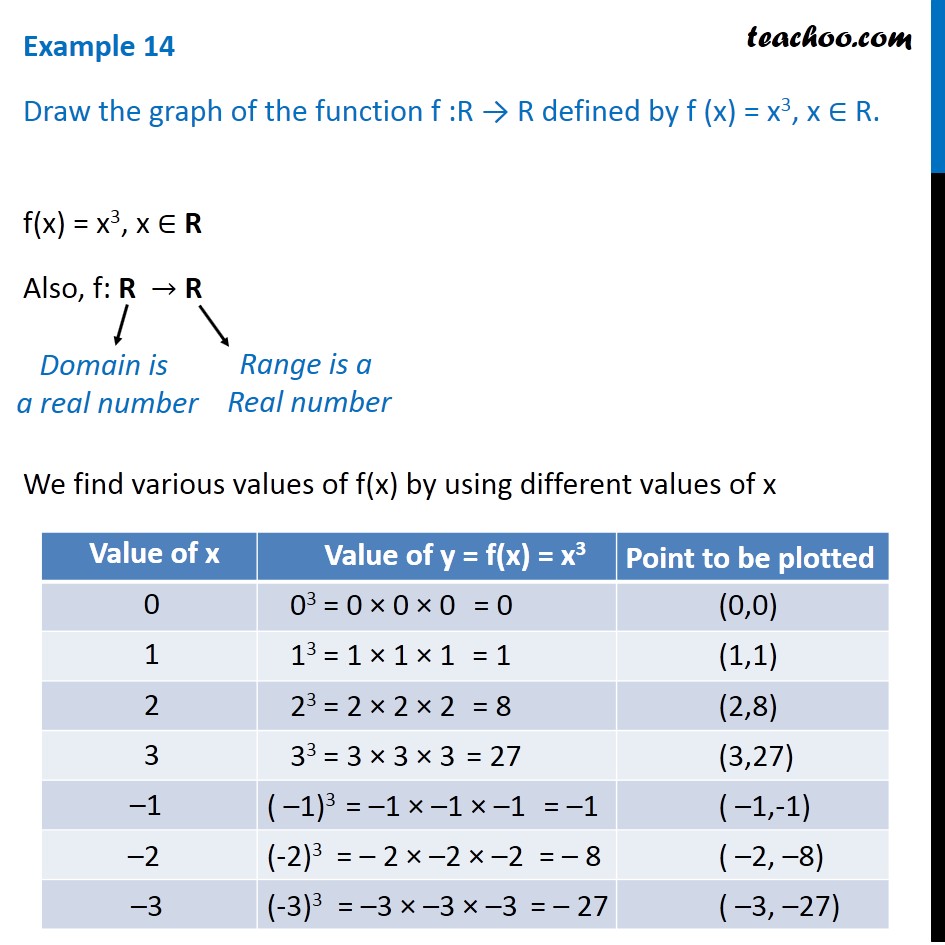



Example 14 Draw Graph Of F X X 3 Chapter 2 Class 11




Finding The Domain And Range Of A Function In Chegg Com



Unit 3 Parent Functions



What Is The Domain And Range For The Following Function And Its Inverse F X 3x 1 2 Mathskey Com



2




Find The Domain And The Range Of The Real Function F X X 3 X 5




Find The Domain And Range Of The Inverse Of The Given Chegg Com



Find The Domain And Range Of F X 2x 5 Mathskey Com




Ws 1 1 Answer Key



The Range Of The Function F X 7 Xpx 3 Is Sarthaks Econnect Largest Online Education Community



2




Find The Domain And Range Of The Function F X X 2 9 X 3
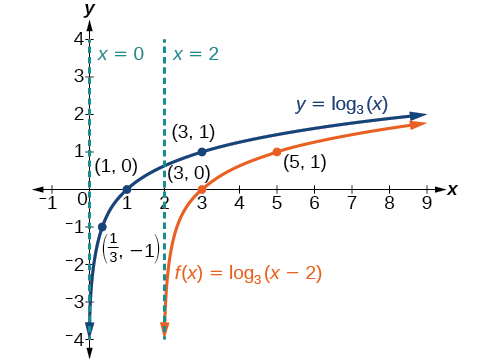



Graphs Of Logarithmic Functions Precalculus



2
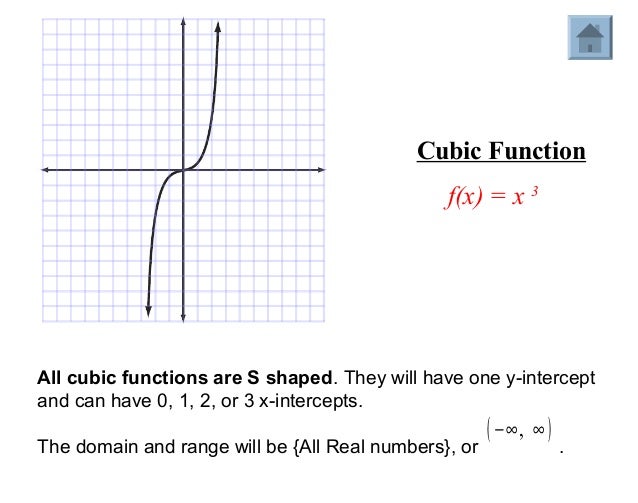



Module 2 Lesson 4 Notes




Introduction To Function Domain And Range Mohd Noor



How Do You Find The Domain And Range Of F X X 4 4x 3 3x 2 Socratic




Lesson 2 Stretches Shrinks And Domain Range Flashcards Quizlet




Exercise 1 3 Functions Problem Questions With Answer Solution



0 件のコメント:
コメントを投稿